问题：

据说着名犹太历史学家Josephus有过以下的故事：在罗马人占领乔塔帕特后，39个犹太人与Josephus及他的朋友躲到一个洞中，

39个犹太人决定宁愿死也不要被敌人找到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到

第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus和他的朋友并不想遵从，Josephus

要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

解法：

约瑟夫问题可用代数分析来求解，将这个问题扩大好了，假设现在您与m个朋友不幸参与了这个游戏，您要如何保护您与您的

朋友？其实只要将阵列当作环状来处理就可以了，在阵列中由计数1开始，每找到第三个就填入一个计数，直到计数达41为止，

然后将阵列由索引1开始列出，就可以得知每个位置的自杀顺序，这就是约瑟夫排列，41个人而报数3的约琴夫排列如下所示：

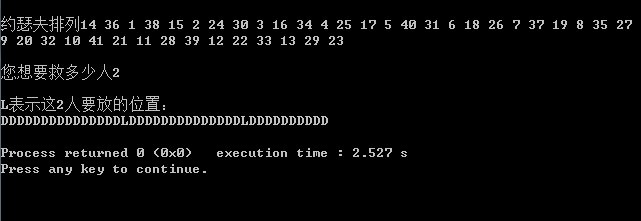
14 36 1 38 15 2 24 30 3 16 34 4 25 17 5 40 316 18 26 7 37 19 8 35 27 9 20 32 10 41 21 11 28 39 12 22 33 13 29 23

由上可知，最后一个自杀的是在第31个位置，而倒数第二个自杀的要排在第16个位置，之前的

人都死光了，所以他们也就不知道约琴夫与他的朋友并没有遵守游戏规则了。

#include <stdio.h>

#include <stdlib.h>

#define N 41

#define M 3

int main(void)

{

    int man[N] = {0};

    int count = 1;

    int i = 0, pos = -1;

    int alive = 0;

    while(count <= N)

    {

        do

        {

            pos = (pos+1) % N; //环状处理

            if(man[pos] == 0)

                i++;

            if(i == M)

            { // 报数为3了

                i = 0;

                break;

            }

        } while(1);

        man[pos] = count;

        count++;

    }

    printf("\n约瑟夫排列");

    for(i = 0; i < N; i++)

        printf("%d ", man[i]);

    printf("\n\n您想要救多少人");

    scanf("%d", &alive);

    printf("\nL表示这%d人要放的位置：\n", alive);

    for(i = 0; i < N; i++)

    {

        if(man[i] < 41-alive+1)

            printf("D");

        else

            printf("L");

    }

    printf("\n");

    return 0;

}

//测试结果：